PageRank is an algorithm used to measure the relative importance of nodes in a graph system. It is the underlying algorithm that determines what the 3.8 billion population of internet users experience on the web today.

PageRank works great on an unweighted graph, i.e. it assumes that all the edges in the graph are of equal importance. However, there are a number of real world scenarios where the relationship between two nodes may differ based on its nature.
If an article on Medium has links to two other independent web pages B & C, the importance of the link may be inferred from where it is located in the article content ( Higher position => More important => more weight ).
Weighted PageRank
In such scenarios, we need to resort to an edge-weighted graph and the PageRank algorithm can be modified to incorporate the edge weights in the calculation.
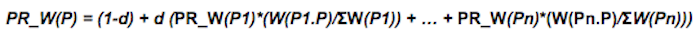
PR_W(p) is the weighted pageRank of P. Here, W(P1.P) denotes the weight of edge from P1 to P, while ΣW(P1) is the total weight of all outgoing edges from P1. If this looks overwhelming to you, i’d suggest you read about the basic pagerank calculation here.
Neo4j is one of the most popular graph databases today. Its intuitive modelling and simple query language (cypher) makes it very easy to represent any system as a Graph system. Neo4j does not provide PageRank computation out of the box, hence one needs to use a third party library APOC which provides a lot of graph algorithms including PageRank which can be run as cypher procedures in Neo4j.
However, the library does not have support for a Weighted PageRank algorithm. Hence, I decided to implement it in cypher, the code gist of which looks like this —
Now PageRank algorithm is inherently an iterative algorithms i.e. the algorithm needs to be iterated over the graph multiple times till the delta ΔPR between successive iterations is negligible. I wrote a simple program in NodeJS that runs this cypher script iteratively and checks for the difference between successive iterations after each execution
Voila! There we have our weighted PageRank algorithm. Have fun incorporating it into your own graphs..